
Copyright © 2026, Molsoft LLC
Feb 18 2026
Google Search:
Keyword Search:| Prev | ICM Language Reference Structure analysis | Next |
[ Superimpose faq | Align 3D faq | Ramachandran faq | Hbonds faq | Interface residues | Res selections | Interface torsions | Packing density | Principal component analysis | Dihedral angle calculation | All torsions table | Hydrophobicity profile | Cavity analysis ]
How to optimally superimpose two 3D structures |
|
Optimal superposition implies optimization of the Ca-RMSD upon
rigid body superposition of the equivalent residues/atoms.
This set of equivalent positions can be predefined, or determined
by sequence alignment, or automatically derived from structure.
In the latter case the optimized value is
the RMSD of a trial alignment is corrected by the alignment length
to reward longer alignment with slightly worse RMSD.
The resulting transformation vector is returned in R_out (see the transform
command) .
There are several different algorithms which can be applied: |
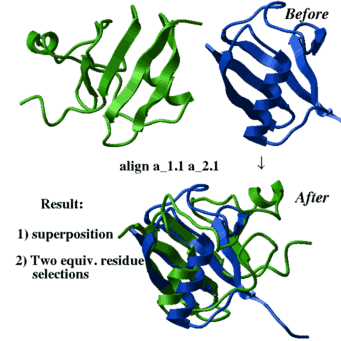
|
- superimpose by known residue or atom equivalences (see the superimpose command)
- superimpose by sequence alignment which is calculated on the fly:
superimpose a_1.1 a_2.1 align # the sequences are generated on the fly superimpose a_1.1 a_2.1 align minimize # even better method
This procedure fails if two structures have no significant sequence similarity - align .. command to find global structural alignment (returned by the ali_out variable)
and superimpose accordingly.
Here we do not rely on sequence alignement (although it can be added to
the optimized scoring function with a certain weight).
align a_1.1 a_2.1 - Align(.. distance) for local structural alignment
Use superimpose command. It performs an optimal rotation and translation of one structure onto the other. If necessary, a sequence alignment may be done prior to superposition by specifying align option in the command line.
Example:
read pdb "3znf"
display a_1.1//n,ca,c magenta
make sequence a_1.1
read pdb "1ard"
display a_2.1//n,ca,c blue
make sequence a_2.1
show sequence
# somewhat different sequences of two Zn-fingers
# sequence alignment is required
superimpose a_1. a_2. align
Note, in this particular example, the whole structural similarity
is not so high. However, better fit may be obtained if only portions
of the structures are superimposed, for example:
superimpose a_1.1/16:27/n,ca,c a_2.1/116:127/n,ca,c align transform g_2_skinGrob R_out # rearrange a related grob accordinglySee also: transform, transformation vector, Rmsd( ) and Srmsd( ).
How to optimally superimpose without the residue alignment |
The core of this procedure is the
align ms_molecule1 ms_molecule2
command. There are two variants: a fast superposition using dynamic programming algorithm align [distance] ms_1 ms_2 or a more rigorous, but somewhat less stable and slow align heavy ms_1 ms_2 ... command. This first command is well described above and identifies only the best superposition. The initial superposition is then refined similarly to the find alignment command.
The second algorithm (option heavy ) identifies a number of possible superpositions (solutions) based on the Ca atom coordinates only. The first solution is the best hit. See also load solution command.
Examples:
read pdb "4fxc" read pdb "1ubq" display a_*.//ca,c,n color molecule a_*. align a_1.1 a_2.1 center color red as_out color blue as2_out show ali_out
How to make a Ramachandran plot |
Use macro plotRamaEps . The macro is invoked by
plotRamaEps rs_selection l_addLabel l_addBoundaries
Important: if a PDB structure is analyzed, convert it first to get a proper ICM-object (true ICM-molecular object does not require prior preparation for building Ramachandran plot).
Example:
read pdb "1crn"
convert a_1. # Note, one more object appeared in addition
# to the original (PDB) object 1crn
l_addLabel = yes # add residue labels to the plot
l_shadedBoundaries = yes # add allowed regions to the plot
plotRamaEps a_2. l_addLabel l_shadedBoundaries
quit
How to display hydrogen bonds |
A list of hydrogen bonds may be calculated and displayed for an ICM-objects or non-ICM object with hydrogens or made into a separate object of atom pair distances with labels. If you are dealing with a PDB structure without hydrogens, convert it first. The command show hbond prints list of hydrogen bonds in the text window. After that they can be displayed. (Hydrogen bonds can also be calculated by minimize and show energy commands provided that the hydrogen bond energy term is switched on.)
The display hbond command allows one to show the deviation angle of the hydroben bond from linearity (see the GRAPHICS.hbondStyle preference ).
Examples:
read object "crn" # already converted
show energy
display
show hbond 2.5 a_/1:15 # list of H-bonds with H-X distance < 2.5 A
# appears in the text window
display hbond 1.9 # H-bonds shorter than 1.9 A are shown
GRAPHICS.hbondStyle = 3
display hbond
See also:
- Table(hbonddist,distance)
- GRAPHICS.hbondAngleSharpness (1.7)
- GRAPHICS.hbondBallPeriod (1.2)
- GRAPHICS.hbondMinStrength (1. , allowed range (0.,2.) )
- GRAPHICS.hbondWidth (0.6)
- GRAPHICS.hbondBallStyle
- GRAPHICS.hbondRebuild
- GRAPHICS.hbondStyle (label style)
How to identify atoms or residues at the molecular interface |
When two or more parts of the polypeptide chain(s) are near each other in space, they are referred to as a molecular interface. What "interface" is can be defined more specifically in the context of a particular study, so here only an example is given to illustrate how interface may be identified and displayed. Two ICM functions are to be used for that, viz. Sphere and Acc . Suppose, you analyze 3D structure of a complex of two molecules, and would like to see what residues are at the interface. It can be done by the following:
read object "complex"
display a_1,2//!h* # display both molecules
# without hydrogens
color a_1 yellow
color a_2 green
show area surface a_1//!h* a_1//!h* # calculate surface of
# the 1st molecule only
color red Sphere(a_2//* a_1//* 4.) & Acc(a_1/*)# interface residue atoms
# of the 1st molecule
# in 4 A radius vicinity
# of the 2nd molecule
show area surface a_2//!h* a_2//!h* # calculate surface of
# the 2nd molecule only
color blue Sphere(a_1//* a_2/* 4.)&Acc(a_2//*) # interface residue atoms
# of the 2nd molecule
# in 4 A radius vicinity
# of the 1st molecule
If, instead, you need to mark residues,
convert the selection of the interface atoms to residues with
the Res () command:
.... # same as above. .... resAtInterf = Res( Sphere(a_2//* a_1//* 4.)) & Acc(a_1/*) display residue label resAtInterfNote that in the Sphere command it does not matter if you specify the atom selection or a residue selection as an argument, since the function operates at the atom level anyway. The difference in the specification of the ICM selection in these two examples (usage of two slashes for atom selection, and one slash for residue selection):
Sphere(a_1.1/* 4.) versus Sphere(a_1.2//* 4.) and also Acc(a_1.1/*) versus Acc(a_1.2//*) for specifying residues and atoms, respectively.
Important: when calculating surface, be sure that you properly specify the selection arguments in the show area surface command.
How to select accessible, buried, hydrophobic, residues. |
Selecting exposed residues. Here is one way to compile a list of exposed residues. Use the Acc ( rs_ [ r_threshold ] ) function. It will return all residues for which relative residue solvent accessibility is larger than certain limit ( by default it is 25% of its fully accessible surface ). To use the function you need to get rid of water molecules and use the show surface are command. Follow this example:
read pdb "1crn" delete a_W # delete water molecules show surface area # compute exposed surface areas for each residue show Acc( a_/* , 0.25 ) # show all residues exposed more than 25%) show !Acc(a_/* , 0.25 ) # show buried residues
Converting the selection into other formats
You can also show the selection in a different format, e.g.
String( Acc( a_/* )) # or a_1crn.m/1,5:8,11:12,14:15,17:20,22:25,28:29,31,33:34,36:46 Label( Acc(a_/*)) #>S string_array T1 P5 S6 I7 V8 S11 ...
Identifying buried polar residues
About 50% of all residues have relative accessibility less than 25%. Polar residues typically do not like to be buried. The charged residues like it even less, and if they are buried they usually form a salt bridge. Example:
read pdb "1qau" # neuronal nitric oxide synthase display display xstick a_/62,121 # buried asp and arg form a bridge
To identify buried charged residues, use combine the previous selection of the buried residues with specific residue type selection, e.g.
read pdb "1qau" delete a_W show surface area show a_/asp,glu,arg,lys & ! Acc( a_/* 0.15 )Here we used a more conservative threshold of 0.15 as the burial threshold. Feel free to modify the selection of residue types above to find other buried residues.
Identifying exposed hydrophobic patches
A similar technique can be used to identify hydrophobic patches:
read pdb "1qau" delete a_W show surface area show a_/leu,ile,val,met,trp & ! Acc( a_/* ) # buried ones show Acc( a_/leu,ile,val,met,trp ) # exposed hydrophobs
To find clusters of exposed hydrophobic residues, use the Sphere function. The Sphere function returns atoms, and they need to be converted to residues with the Res function.
exposed_hres = Acc( a_/leu,ile,val,met,trp )
for i=1,Nof(exposed_hres )
nbrs = Res(Sphere( exposed_hres[i] exposed_hres , 5.0 ))
if Nof( nbrs ) >= 2 show nbrs # show pairs of exposed hydrophobs
endfor
How to identify torsions at the molecular interface |
Identification of the torsions belonging to residues at the molecular interface is a necessary and non-trivial step in many tasks of the molecular modeling. An example below shows how this identification may be done in ICM. The same as above ICM-object "complex" is considered.
read object "complex"
display a_1.1,2//!h* # display both molecules
# of the complex w/o hydrogens
color a_1.1 yellow
color a_1.2 green
show area surface a_1.1//!h* a_1.1//!h* # calculate surface of
# the 1st molecule only
a1=Sphere(a_1.2//* 7.) & Acc(a_1.1//*) # define the 1st molecule atoms
# belonging to the interface
# of the 1st molecule
# in 7 A radius vicinity
v1=V_1.1//S & a1 # identify standard geometry
# torsions of the 1st molecule
# belonging to the interface
color red Atom(v1) # color atoms which torsions
# belong to
# similar for the 2nd molecule
show area surface a_1.2//!h* a_1.2//!h*
a2=Sphere(a_1.1//* 7.) & Acc(a_1.2//*)
v2=V_1.2//S & a2
color blue Atom(v2)
How to calculate packing density |
The packing density analysis requires understanding of two types of surfaces: the skin (molecular surface) and solvent-accessible surface of water probe centers (which is one water radius away from the skin ). The following is an example of how it may be done for a fragment of a protein.
read object s_icmhome+"crn" asel = a_/5:15 show volume skin asel rskin = r_out vwExpand = 0. show volume surface asel rsurf = r_out print "skin volume = ", rskin, "; vw volume = ", rsurf print "packing density = ", rskin/rsurf
How to perform a principal component analysis |
For a set of objects with given measure of similarity between each two of them, one can easily perform the principal component analysis or to solve a distance geometry problem by using Disgeo function. The following example shows how to get a two-dimensional distribution of amino acid sequences of a series of Zn-fingers given the distance between sequences is defined by Distance( sequence1 sequence2 ) function. This distance is essentially a measure of sequence similarity: the distance is 0. for two identical sequences, it is proportional to percent identity divided by 100. for very similar sequences and goes above one at about 30% sequence identity, tending to infinity for very small seq. identity numbers.
read sequences s_icmhome+"zincFing" # read sequences from file,
list sequences # see them, then ...
group sequence alZnFing # group them, then ...
align alZnFing # align them, then ...
a = Distance(alZnFing) # calculate a matrix of pairwise
# distances among them
n=Nof(a) # number of points
b=Disgeo(a) # calculate principal components
corMat = b[1:n,1:n-1] # coordinate matrix [n,n-1] of n points
eigenV = b[1:n,n] # vector with n sorted eigenvalues
xplot = corMat[1:n,1]
yplot = corMat[1:n,2]
# plot 2D distribution
plot xplot yplot CIRCLE display
How to calculate a dihedral angle |
Normal dihedral angles like torsion angles describing conformation are directly available through the Value( ) function. You need to convert an object into the ICM type if necessary.
Example:
read pdb "1crn" # read it in convert # quickly convert into ICM-object show v_//phi,psi # just show all phi,psi's show v_/3:17/xi* # show chi angles of residues from 3 to 17 a = Value(v_//phi,psi) # create a real array of values of spec. torsionsYou can calculate a dihedral angle between any two planes defined by three atoms (for example two Phe rings) with the calcDihedralAngle macro. If this macro is loaded, you can do the following:
read object "crn" as_1 = a_/1/n,ca,c as_2 = a_/3/n,ca,c display a_//n,ca,c blue color as_1 magenta color as_2 green calcDihedralAngle as_1 as_2 print "dihedral angle 1(n,ca,c) and 3(n,ca,c) (deg) = ", r_outNote that the order of atoms in the selections as_1 and as_2 is determined only by the ICM-molecular tree (will be the same for a_//n,c or a_//c,n). Thus, any changes in the selections as_1 and as_2 not changing their content has no effect on the resulting dihedral angle:
as_1 = a_/1/ca,c,n as_2 = a_/3/ca,c,n calcDihedralAngle as_1 as_2 print "dihedral angle 1(n,ca,c) and 3(n,ca,c) (deg) = ", r_outSee also: Acos( ), Length( ), Sum( ), Vector( ).
How to print a table of the torsion angles |
The simplest list can be generated by:
show V_//* # or show V_//phi*,psi*,omg* # or show V_//xi* # side chain torsionsA nicer formatted output (one line per residue) may be generated with macro printTorsions, for example:
read pdb "1crn" convert printTorsions a_/2:15Note, that you do not need to convert your molecular object if it is an ICM-object.
How to build a hydrophobicity profile |
First, define a hydrophobicity scale, for example that from Kyte and Doolittle, 1982 or use your favorite one. (Note, there should be 26 entries in the hydrophobicity parameters list hPhobInd corresponding to the 26 letters of the alphabet. Non-participating letters B,J,O,U,X,Z are marked by zero values.)
# define a hydrophobicity scale
hPhobInd = { 1.8, 0.0, 2.5, -3.5, -3.5, 2.8, -0.4, \
-3.2, 4.5, 0.0, -3.9, 3.8, 1.9, -3.5, \
0.0, -1.6, -3.5, -4.5, -0.8, -0.7, 0.0, \
4.2, -0.9, 0.0, -1.3, 0.0}
# make a macro
macro hPhobProfile seq_ i_windowSize
if (Type(i_windowSize)=="unknown") then
i_windowSize = Ask("Enter window size",windowSize)
endif
R_window = Rarray(i_windowSize,1./i_windowSize)
R_hphob = Smooth (Rarray(seq_,hPhobInd), R_window)
R_ruler = {0.,0.,10.,10.,0.,0.,0.,0.}
R_ruler[2] = Real(Length(seq_))
r_tic = 1./Sqrt(Real(i_windowSize))
r_tic = Integer(r_tic*100.0)/100.
R_ruler[5] = -7.*r_tic
R_ruler[6] = 7.*r_tic
R_ruler[7] = r_tic
R_ruler[8] = r_tic
print R_ruler
s_legend = {"Hydrophobicity plot","Sequence","Hydrophobicity"}
xplot = Count(1 Length(seq_))
yplot = R_hphob
psfilename = "hphob"
plot xplot yplot R_ruler s_legend grid="xy" display psfilename
delete R_window R_ruler r_tic
endmacro
# now, an example
read object "crn"
s = Sequence(a_)
hPhobProfile s 7
How to display and characterize protein cavities |
ICM offers fast, elegant and mathematically accurate way to identify, display, and measure protein cavities. An example session which displays all cavities with their surroundings, and calculates their volumes and surface areas:
Examples:
read object "crn" # or whatever
make grob skin "g_skin"
split g_skin
nShells = i_out
display wire residue labels
for i=1,nShells
v = Volume(g_skin$i) # actually its surface is returned in r_out
s = r_out # there is no need to use the explicit Area(g_skin$i)
if(v > 0.) then # note that cavities have negative volume!
display transparent smooth g_skin$i
printf "Shell %d: V=%f A=%f\n", i, v, s
else
display reverse smooth yellow g_skin$i
center g_skin$i
printf "CAVITY %d: V=%f A=%f R~%f\n", i, -v, s, -3.*v/s
endif
# add pause here for an interactive session
endfor
| Prev Color by charge | Home Up | Next Sequence |